The exponential-family random graph models (ERGMs) have emerged as an important framework for modeling a wide variety of relational types. ERGMs for valued networks are less well-developed than their unvalued counterparts, and pose particular computational challenges. Network data with edge values on the non-negative integers (count-valued networks) is an important such case, with examples ranging from the magnitude of migration and trade flows between places to the frequency of interactions and encounters between individuals.
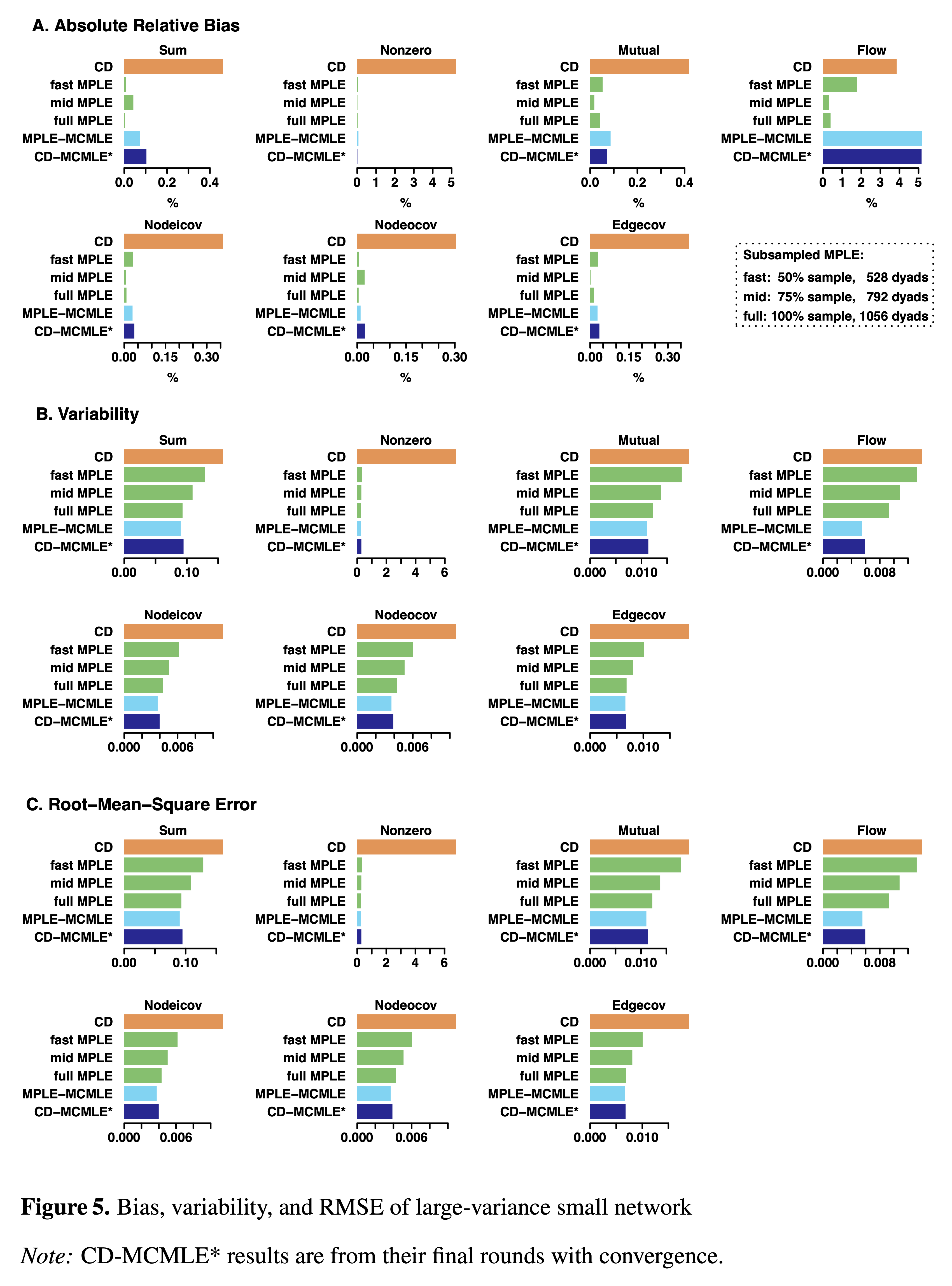
In a recent paper published in Social Networks, NCASD researchers Peng Huang and Carter Butts propose an efficient parallelable subsampled maximum pseudo-likelihood estimation (MPLE) scheme for count-valued ERGMs, and compare its performance with existing Contrastive Divergence (CD) and Monte Carlo Maximum Likelihood Estimation (MCMLE) approaches via a simulation study based on migration flow networks in two U.S. states. Results suggest that edge value variance is a key factor in method performance, while network size mainly influences their relative merits in computational time. MCMLE excels when the edge variance is small, but MPLE performs better for large edge-variance networks. The paper concludes with a guidance for choosing computational methods for valued ERGMs based on data structure, available computational resources and analytical goals.